Gerhard Böhm
Internet Galerie
© Copyright G. Böhm
Internet Galerie
© Copyright G. Böhm
Raum B
Grafiken/Radierungen
Mappenwerk PQ 21
Inhalt: 12 Blätter DIN A3, Pigmenttusche auf 180g Karton
Auflage: 20 Exemplare, signiert und numeriert
© März 2004 Gerhard Böhm, Himmelkron
 Rue la guènèsie |
 Silhouetten |
 Landschaft 2 |
 Suchtrupp |
 Portrait H. N. |
 Ingenieur H. |
 Barszene |
 Räderwerk |
 die Schaukel |
 Strawinsky, Picasso, .. |
 Notizen |
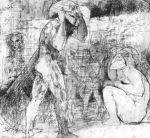 Begegnung zweier ... |
 Picini |
 Kilometer 5 |
 Folketspark 1 |
PQ21 - Mappenwerk von Gerhard Böhm
Perfektes Quadrat 21
Perfektes Quadrat 21
Als perfektes Quadrat bezeichnet man in der Mathematik eine
vollständige Unterteilung eines Quadrats in kleinere Quadrate
paarweise verschiedener Größe. Im Jahr 1962 bewiesen C.J. Bouwkamp,
A.J.W. Duijvestijn und P. Medema, daß es kein perfektes Quadrat
mit weniger als 21 Teilquadraten gibt. Duijvestijn entdeckete
1978 mit Hilfe des Computers ein perfektes Quadrat der Ordnung 21
und zeigte, daß es genau ein solches gibt. Die mathematische
Logik und das Einmalige der Form besitzt eine hohe ästhetische
Wertigkeit und regte mich zur kreativen Nutzung dieser Qualitäten
an. So wurde diese Flächenfügung Grundlage einer computerunterstützten
Werkreihe. Die Wechselwirkung zwischen Form und Farbgebung sind
Inhalt der in Zusammenarbeit mit dem Mathematiker Janko Böhm
entstandenen Werkreihe aus Farbvariationen und Permutationen.
Die vorliegende Mappe zeigt anhand von 12 Blättern Beispiele
dieser Arbeit.
 PQ21-01 |
 PQ21-02 |
 PQ21-03 |
 PQ21-04 |
 PQ21-05 |
 PQ21-06 |
 PQ21-07 |
 PQ21-08 |
 PQ21-09 |
 PQ21-10 |
 PQ21-11 |
 PQ21-12 |